Trigonometri

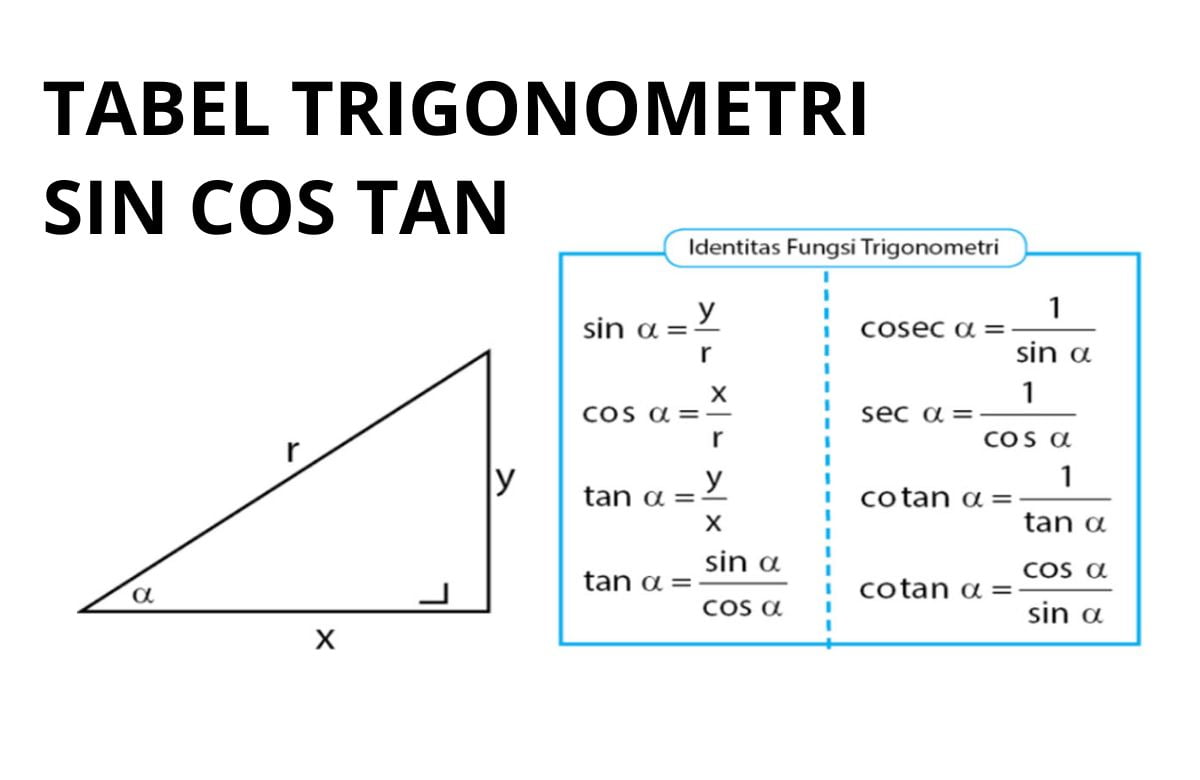
Pewarta Nusantara - Trigonometri adalah cabang Matematika yang mempelajari hubungan antara sudut dan panjang sisi dalam segitiga. Dalam Trigonometri, terdapat tiga fungsi trigonometri dasar yang sangat penting, yaitu sin (sinus), cos (kosinus), dan tan (tangen). Ketiga fungsi ini digunakan untuk menghitung perbandingan antara panjang sisi segitiga dengan sudut yang terkait.
Apa itu sin, cos, dan tan?
Sin (sinus) adalah fungsi trigonometri yang menggambarkan perbandingan panjang sisi miring (disebut juga sebagai opasitas) terhadap panjang sisi miring terpanjang dalam segitiga siku-siku.

Cos (kosinus) menggambarkan perbandingan panjang sisi yang berseberangan dengan sudut yang dimaksud terhadap panjang sisi miring terpanjang.

Sementara itu, tan (tangen) menggambarkan perbandingan antara panjang sisi miring terpendek dengan panjang sisi yang berseberangan dengan sudut yang dimaksud.
Konsep dasar sudut dalam trigonometri
Dalam trigonometri, sudut diukur dalam derajat atau radian. Derajat adalah unit pengukuran sudut yang paling umum digunakan, di mana satu lingkaran penuh dibagi menjadi 360 derajat. Sedangkan radian adalah unit pengukuran sudut yang berdasarkan panjang lengkung pada lingkaran. Terdapat hubungan konversi antara derajat dan radian, yaitu 1 lingkaran penuh = 360 derajat = 2π radian.
Pentingnya Sin Cos Tan dalam matematika dan Fisika
Fungsi sin cos tan memiliki peranan penting dalam berbagai bidang, terutama dalam matematika dan fisika. Dalam matematika, fungsi trigonometri ini digunakan untuk mempelajari hubungan geometri dalam segitiga serta memecahkan berbagai permasalahan yang melibatkan sudut. Dalam fisika, sin cos tan sering digunakan untuk menganalisis dan memodelkan fenomena gelombang, pergerakan benda, osilasi, dan banyak lagi.

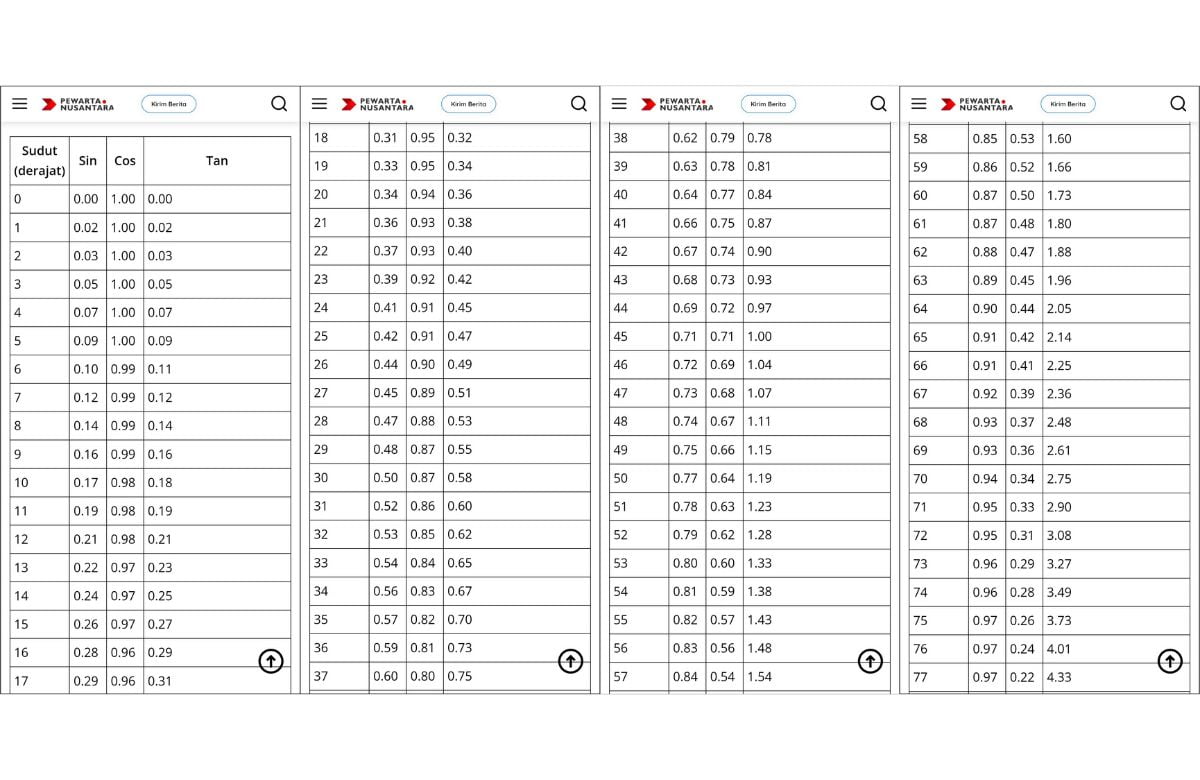
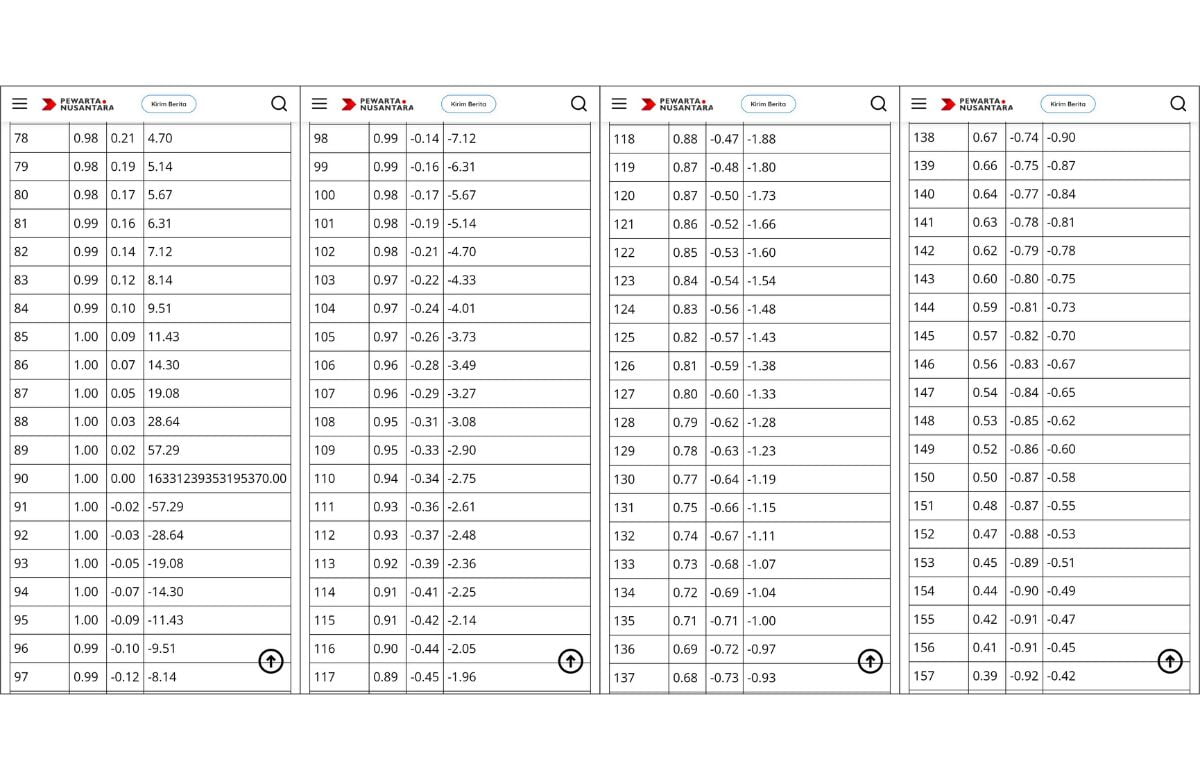
Tabel Sin Cos Tan Lengkap

Mengenal Fungsi Sinus (Sin)
Definisi sin dan rumusnya
Fungsi sinus (sin) dari suatu sudut dalam trigonometri didefinisikan sebagai perbandingan panjang sisi miring terhadap panjang sisi miring terpanjang dalam segitiga siku-siku. Rumus sin dapat dinyatakan sebagai sin(θ) = panjang sisi miring / panjang sisi miring terpanjang.
Grafik sin dan sifat-sifatnya
Grafik sin memiliki pola gelombang yang berulang dari 0 hingga 2π radian (atau 0 hingga 360 derajat). Grafik sin memiliki sifat periodik, simetri terhadap sumbu x, serta nilai maksimum dan minimum pada titik-titik tertentu.
Contoh penggunaan sin dalam perhitungan sudut
Misalnya, jika kita ingin menghitung sin dari sudut 30 derajat, kita dapat menggunakan rumus sin(30°) = panjang sisi miring / panjang sisi miring terpanjang. Dalam kasus ini, sin(30°) = 0.5, yang berarti panjang sisi miring adalah setengah dari panjang sisi miring terpanjang.
Mengenal Fungsi Kosinus (Cos)
Definisi cos dan rumusnya
Fungsi kosinus (cos) merupakan perbandingan panjang sisi yang berseberangan dengan sudut tertentu terhadap panjang sisi miring terpanjang dalam segitiga siku-siku. Rumus cos dapat dinyatakan sebagai cos(θ) = panjang sisi yang berseberangan / panjang sisi miring terpanjang.
Grafik cos dan sifat-sifatnya
Grafik cos juga memiliki pola gelombang yang berulang dari 0 hingga 2π radian (atau 0 hingga 360 derajat). Grafik cos memiliki sifat periodik, simetri terhadap sumbu y, serta nilai maksimum dan minimum pada titik-titik tertentu.
Contoh penggunaan cos dalam perhitungan sudut
Sebagai contoh, jika kita ingin menghitung cos dari sudut 45 derajat, kita dapat menggunakan rumus cos(45°) = panjang sisi yang berseberangan / panjang sisi miring terpanjang. Dalam kasus ini, cos(45°) = 0.707, yang berarti panjang sisi yang berseberangan adalah sekitar 0.707 kali panjang sisi miring terpanjang.
Mengenal Fungsi Tangen (Tan)
Definisi tan dan rumusnya
Fungsi tangen (tan) adalah perbandingan antara panjang sisi miring terpendek dan panjang sisi yang berseberangan dengan sudut tertentu dalam segitiga siku-siku. Rumus tan dapat dinyatakan sebagai tan(θ) = panjang sisi miring terpendek / panjang sisi yang berseberangan.
Grafik tan dan sifat-sifatnya
Grafik tan memiliki pola yang berulang setiap π radian (180 derajat). Grafik tan memiliki asimtot pada sudut-sudut tertentu dan dapat mencapai nilai tak terhingga pada beberapa sudut.
Contoh penggunaan tan dalam perhitungan sudut
Misalnya, jika kita ingin menghitung tan dari sudut 60 derajat, kita dapat menggunakan rumus tan(60°) = panjang sisi miring terpendek / panjang sisi yang berseberangan. Dalam kasus ini, tan(60°) = 1.732, yang berarti panjang sisi miring terpendek adalah sekitar 1.732 kali panjang sisi yang berseberangan.
Hubungan Antara Sin Cos Tan
Persamaan dasar sin, cos, dan tan
Terdapat hubungan yang erat antara sin, cos, dan tan dalam trigonometri. Hubungan tersebut dapat dinyatakan dalam bentuk persamaan dasar trigonometri, yaitu sin^2(θ) + cos^2(θ) = 1 dan tan(θ) = sin(θ) / cos(θ).
Contoh perhitungan yang melibatkan sin cos tan secara bersamaan
Dalam banyak perhitungan trigonometri, kita sering menggunakan sin, cos, dan tan secara bersamaan untuk mencari nilai sudut atau panjang sisi yang tidak diketahui dalam segitiga. Contohnya adalah mencari panjang sisi miring dalam segitiga jika kita mengetahui sudut dan panjang sisi yang diketahui.
Baca juga: Limas Segi Empat: Mengenal Bentuk dan Sifatnya
Penerapan sin cos tan dalam trigonometri
Contoh Penerapan Sin Cos Tan
Sin cos tan memiliki berbagai penerapan dalam trigonometri. Salah satu penerapannya adalah dalam perhitungan sudut dan panjang sisi dalam segitiga, baik segitiga siku-siku maupun segitiga umum. Selain itu, sin cos tan juga digunakan dalam perhitungan trigonometri lanjutan seperti vektor, kompleks, dan transformasi.
Penggunaan sin cos tan dalam geometri
Dalam geometri, sin cos tan digunakan untuk mempelajari sifat-sifat segitiga, menghitung luas segitiga, menentukan ukuran sudut dalam bangun datar, serta menyelesaikan masalah trigonometri dalam bentuk aplikasi geometri.
Penerapan sin cos tan dalam fisika
Dalam fisika, sin cos tan digunakan untuk menganalisis pergerakan benda, gelombang, osilasi, optik, dan berbagai fenomena lainnya. Misalnya, sin cos tan dapat digunakan untuk menghitung pergerakan benda yang bergerak melingkar atau menghitung amplitude osilasi pada pegas.
Contoh kasus nyata yang menggunakan sin cos tan
Ada banyak kasus nyata di mana sin cos tan digunakan untuk memecahkan masalah. Beberapa contoh kasus termasuk penggunaan sin cos tan dalam navigasi kapal, perencanaan bangunan, astronomi, pemetaan lahan, dan rekayasa suara.
Tips dan Trik Menggunakan Sin Cos Tan
Rumus dan identitas trigonometri yang berguna
Dalam menggunakan sin cos tan, penting untuk memahami rumus-rumus trigonometri dan identitas yang berguna. Beberapa contoh rumus yang berguna termasuk identitas Pythagoras, rumus sudut ganda, rumus sudut setengah, serta rumus-rumus yang terkait dengan fungsi trigonometri lainnya.
Strategi untuk menghitung sudut dengan sin cos tan
Terkadang, kita perlu menghitung sudut berdasarkan nilai sin, cos, atau tan yang diketahui. Dalam artikel ini, akan dibahas beberapa strategi dan teknik untuk menghitung sudut dengan menggunakan sin cos tan.
Sumber daya online yang membantu dalam perhitungan sin cos tan
Dalam era digital saat ini, terdapat banyak sumber daya online yang dapat membantu dalam perhitungan sin cos tan. Beberapa contohnya adalah kalkulator trigonometri online, tutorial video, dan situs web pendidikan yang menyediakan materi dan latihan mengenai trigonometri.

Dengan memahami pengenalan sin cos tan, konsep dasar sudut dalam trigonometri, pentingnya sin cos tan dalam matematika dan fisika, serta penerapan dan tips menggunakan sin cos tan, Anda akan memiliki dasar yang kuat dalam mempelajari dan menggunakan fungsi trigonometri ini dalam berbagai bidang.