Matematika

Pewarta Nusantara - Trigonometri adalah cabang Matematika yang mempelajari hubungan antara sudut dan panjang sisi dalam segitiga. Dalam Trigonometri, terdapat tiga fungsi trigonometri dasar yang sangat penting, yaitu sin (sinus), cos (kosinus), dan tan (tangen). Ketiga fungsi ini digunakan untuk menghitung perbandingan antara panjang sisi segitiga dengan sudut yang terkait.
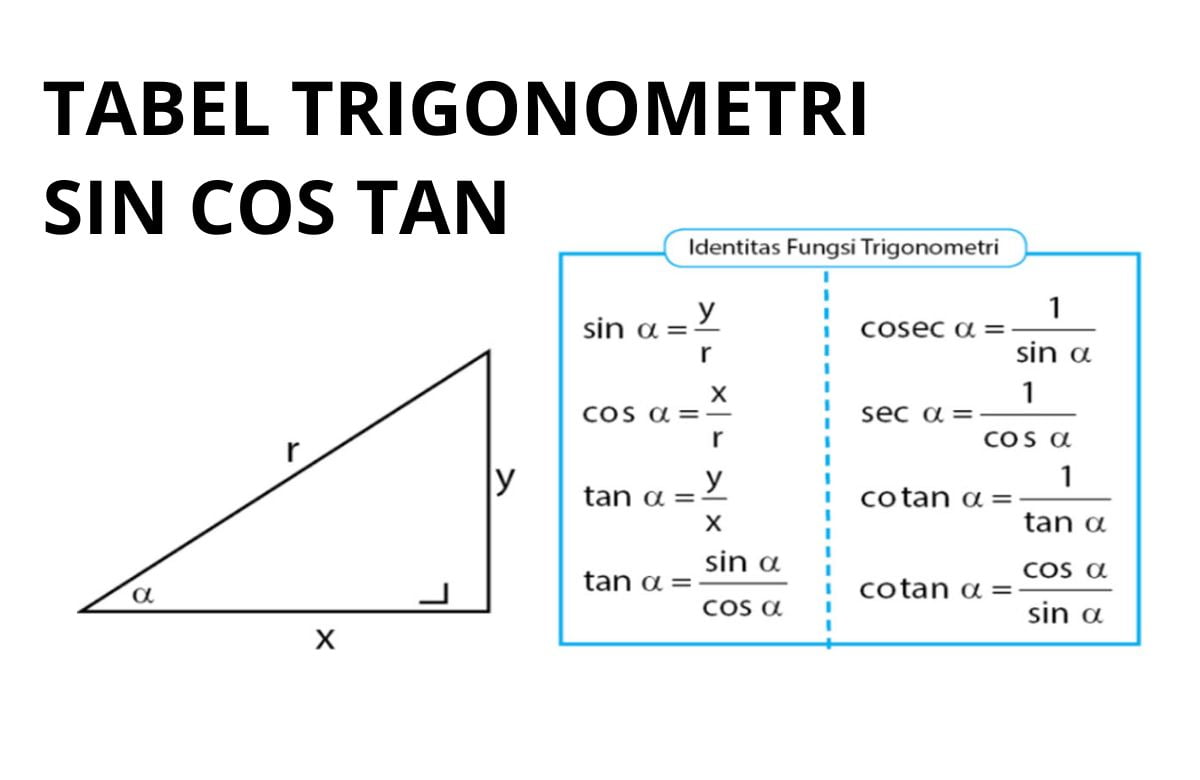
Apa itu sin, cos, dan tan?
Sin (sinus) adalah fungsi trigonometri yang menggambarkan perbandingan panjang sisi miring (disebut juga sebagai opasitas) terhadap panjang sisi miring terpanjang dalam segitiga siku-siku.

Cos (kosinus) menggambarkan perbandingan panjang sisi yang berseberangan dengan sudut yang dimaksud terhadap panjang sisi miring terpanjang.

Sementara itu, tan (tangen) menggambarkan perbandingan antara panjang sisi miring terpendek dengan panjang sisi yang berseberangan dengan sudut yang dimaksud.
Konsep dasar sudut dalam trigonometri
Dalam trigonometri, sudut diukur dalam derajat atau radian. Derajat adalah unit pengukuran sudut yang paling umum digunakan, di mana satu lingkaran penuh dibagi menjadi 360 derajat. Sedangkan radian adalah unit pengukuran sudut yang berdasarkan panjang lengkung pada lingkaran. Terdapat hubungan konversi antara derajat dan radian, yaitu 1 lingkaran penuh = 360 derajat = 2π radian.
Pentingnya Sin Cos Tan dalam matematika dan Fisika
Fungsi sin cos tan memiliki peranan penting dalam berbagai bidang, terutama dalam matematika dan fisika. Dalam matematika, fungsi trigonometri ini digunakan untuk mempelajari hubungan geometri dalam segitiga serta memecahkan berbagai permasalahan yang melibatkan sudut. Dalam fisika, sin cos tan sering digunakan untuk menganalisis dan memodelkan fenomena gelombang, pergerakan benda, osilasi, dan banyak lagi.

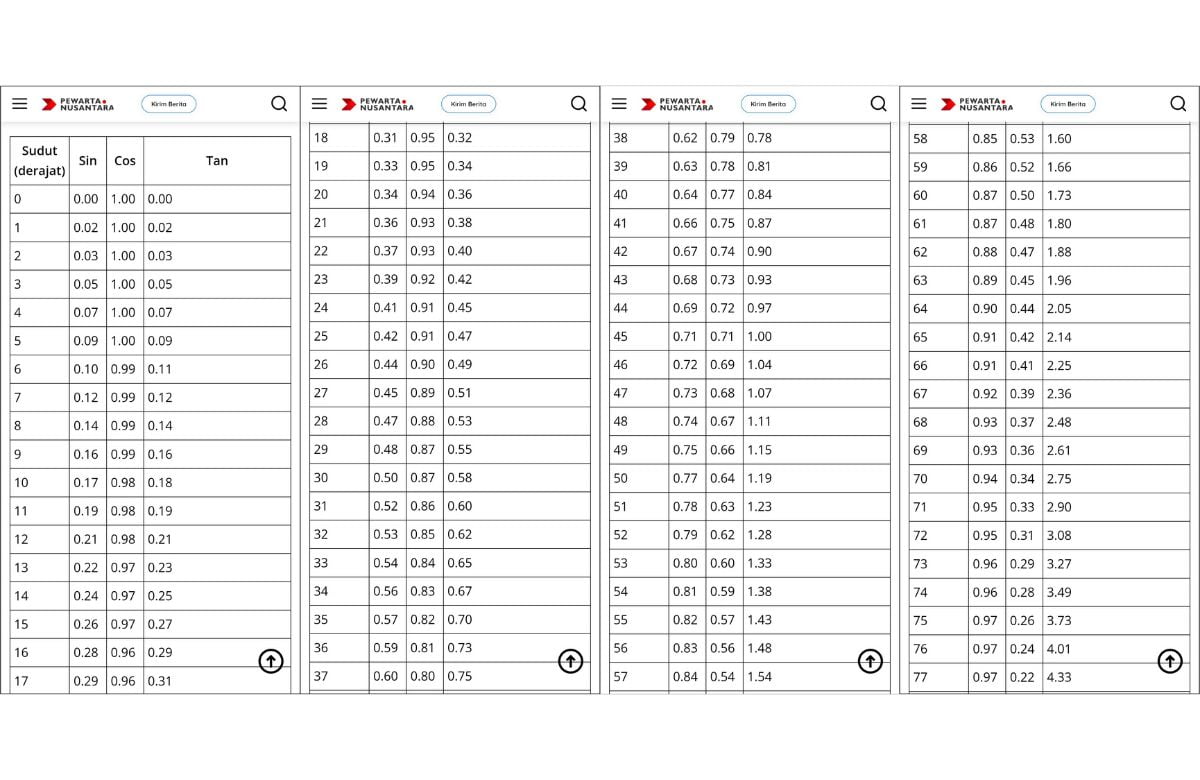
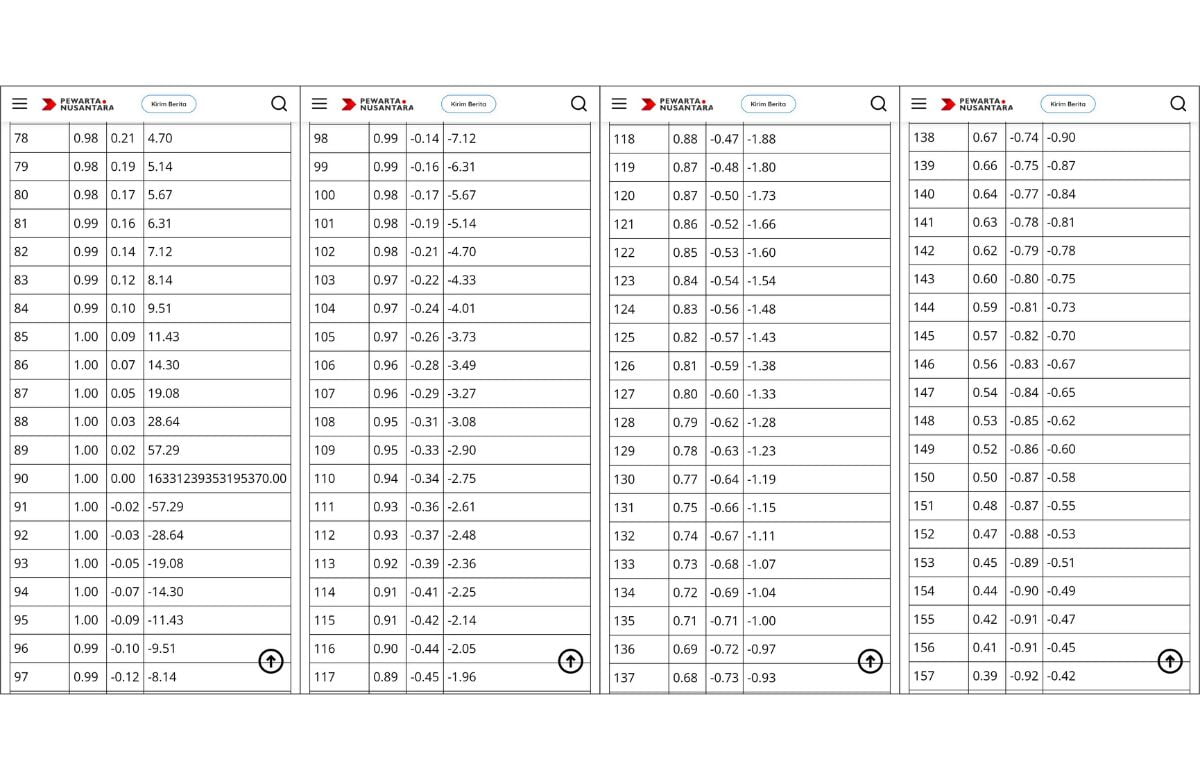
Tabel Sin Cos Tan Lengkap

Mengenal Fungsi Sinus (Sin)
Definisi sin dan rumusnya
Fungsi sinus (sin) dari suatu sudut dalam trigonometri didefinisikan sebagai perbandingan panjang sisi miring terhadap panjang sisi miring terpanjang dalam segitiga siku-siku. Rumus sin dapat dinyatakan sebagai sin(θ) = panjang sisi miring / panjang sisi miring terpanjang.
Grafik sin dan sifat-sifatnya
Grafik sin memiliki pola gelombang yang berulang dari 0 hingga 2π radian (atau 0 hingga 360 derajat). Grafik sin memiliki sifat periodik, simetri terhadap sumbu x, serta nilai maksimum dan minimum pada titik-titik tertentu.
Contoh penggunaan sin dalam perhitungan sudut
Misalnya, jika kita ingin menghitung sin dari sudut 30 derajat, kita dapat menggunakan rumus sin(30°) = panjang sisi miring / panjang sisi miring terpanjang. Dalam kasus ini, sin(30°) = 0.5, yang berarti panjang sisi miring adalah setengah dari panjang sisi miring terpanjang.
Mengenal Fungsi Kosinus (Cos)
Definisi cos dan rumusnya
Fungsi kosinus (cos) merupakan perbandingan panjang sisi yang berseberangan dengan sudut tertentu terhadap panjang sisi miring terpanjang dalam segitiga siku-siku. Rumus cos dapat dinyatakan sebagai cos(θ) = panjang sisi yang berseberangan / panjang sisi miring terpanjang.
Grafik cos dan sifat-sifatnya
Grafik cos juga memiliki pola gelombang yang berulang dari 0 hingga 2π radian (atau 0 hingga 360 derajat). Grafik cos memiliki sifat periodik, simetri terhadap sumbu y, serta nilai maksimum dan minimum pada titik-titik tertentu.
Contoh penggunaan cos dalam perhitungan sudut
Sebagai contoh, jika kita ingin menghitung cos dari sudut 45 derajat, kita dapat menggunakan rumus cos(45°) = panjang sisi yang berseberangan / panjang sisi miring terpanjang. Dalam kasus ini, cos(45°) = 0.707, yang berarti panjang sisi yang berseberangan adalah sekitar 0.707 kali panjang sisi miring terpanjang.
Mengenal Fungsi Tangen (Tan)
Definisi tan dan rumusnya
Fungsi tangen (tan) adalah perbandingan antara panjang sisi miring terpendek dan panjang sisi yang berseberangan dengan sudut tertentu dalam segitiga siku-siku. Rumus tan dapat dinyatakan sebagai tan(θ) = panjang sisi miring terpendek / panjang sisi yang berseberangan.
Grafik tan dan sifat-sifatnya
Grafik tan memiliki pola yang berulang setiap π radian (180 derajat). Grafik tan memiliki asimtot pada sudut-sudut tertentu dan dapat mencapai nilai tak terhingga pada beberapa sudut.
Contoh penggunaan tan dalam perhitungan sudut
Misalnya, jika kita ingin menghitung tan dari sudut 60 derajat, kita dapat menggunakan rumus tan(60°) = panjang sisi miring terpendek / panjang sisi yang berseberangan. Dalam kasus ini, tan(60°) = 1.732, yang berarti panjang sisi miring terpendek adalah sekitar 1.732 kali panjang sisi yang berseberangan.
Hubungan Antara Sin Cos Tan
Persamaan dasar sin, cos, dan tan
Terdapat hubungan yang erat antara sin, cos, dan tan dalam trigonometri. Hubungan tersebut dapat dinyatakan dalam bentuk persamaan dasar trigonometri, yaitu sin^2(θ) + cos^2(θ) = 1 dan tan(θ) = sin(θ) / cos(θ).
Contoh perhitungan yang melibatkan sin cos tan secara bersamaan
Dalam banyak perhitungan trigonometri, kita sering menggunakan sin, cos, dan tan secara bersamaan untuk mencari nilai sudut atau panjang sisi yang tidak diketahui dalam segitiga. Contohnya adalah mencari panjang sisi miring dalam segitiga jika kita mengetahui sudut dan panjang sisi yang diketahui.
Baca juga: Limas Segi Empat: Mengenal Bentuk dan Sifatnya
Penerapan sin cos tan dalam trigonometri
Contoh Penerapan Sin Cos Tan
Sin cos tan memiliki berbagai penerapan dalam trigonometri. Salah satu penerapannya adalah dalam perhitungan sudut dan panjang sisi dalam segitiga, baik segitiga siku-siku maupun segitiga umum. Selain itu, sin cos tan juga digunakan dalam perhitungan trigonometri lanjutan seperti vektor, kompleks, dan transformasi.
Penggunaan sin cos tan dalam geometri
Dalam geometri, sin cos tan digunakan untuk mempelajari sifat-sifat segitiga, menghitung luas segitiga, menentukan ukuran sudut dalam bangun datar, serta menyelesaikan masalah trigonometri dalam bentuk aplikasi geometri.
Penerapan sin cos tan dalam fisika
Dalam fisika, sin cos tan digunakan untuk menganalisis pergerakan benda, gelombang, osilasi, optik, dan berbagai fenomena lainnya. Misalnya, sin cos tan dapat digunakan untuk menghitung pergerakan benda yang bergerak melingkar atau menghitung amplitude osilasi pada pegas.
Contoh kasus nyata yang menggunakan sin cos tan
Ada banyak kasus nyata di mana sin cos tan digunakan untuk memecahkan masalah. Beberapa contoh kasus termasuk penggunaan sin cos tan dalam navigasi kapal, perencanaan bangunan, astronomi, pemetaan lahan, dan rekayasa suara.
Tips dan Trik Menggunakan Sin Cos Tan
Rumus dan identitas trigonometri yang berguna
Dalam menggunakan sin cos tan, penting untuk memahami rumus-rumus trigonometri dan identitas yang berguna. Beberapa contoh rumus yang berguna termasuk identitas Pythagoras, rumus sudut ganda, rumus sudut setengah, serta rumus-rumus yang terkait dengan fungsi trigonometri lainnya.
Strategi untuk menghitung sudut dengan sin cos tan
Terkadang, kita perlu menghitung sudut berdasarkan nilai sin, cos, atau tan yang diketahui. Dalam artikel ini, akan dibahas beberapa strategi dan teknik untuk menghitung sudut dengan menggunakan sin cos tan.
Sumber daya online yang membantu dalam perhitungan sin cos tan
Dalam era digital saat ini, terdapat banyak sumber daya online yang dapat membantu dalam perhitungan sin cos tan. Beberapa contohnya adalah kalkulator trigonometri online, tutorial video, dan situs web pendidikan yang menyediakan materi dan latihan mengenai trigonometri.

Dengan memahami pengenalan sin cos tan, konsep dasar sudut dalam trigonometri, pentingnya sin cos tan dalam matematika dan fisika, serta penerapan dan tips menggunakan sin cos tan, Anda akan memiliki dasar yang kuat dalam mempelajari dan menggunakan fungsi trigonometri ini dalam berbagai bidang.

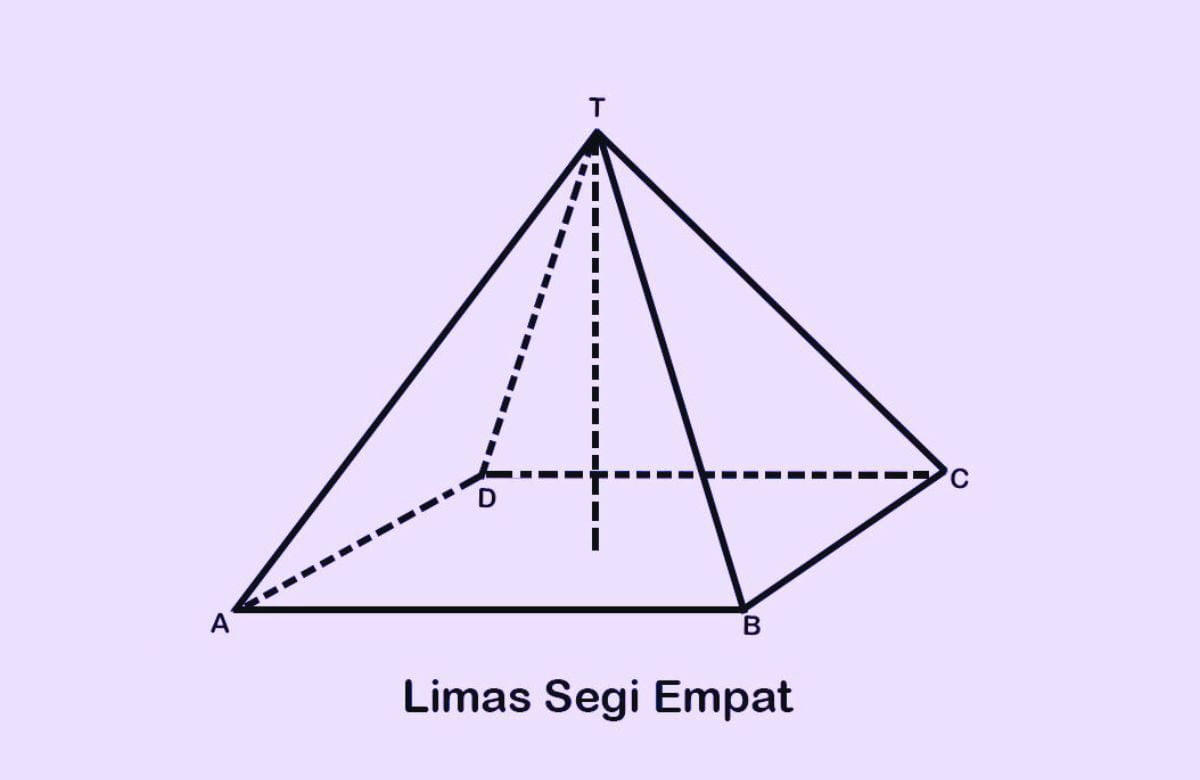
Pewarta Nusantara - Limas Segi Empat adalah Bentuk geometri yang merupakan salah satu konsep dasar dalam Matematika.

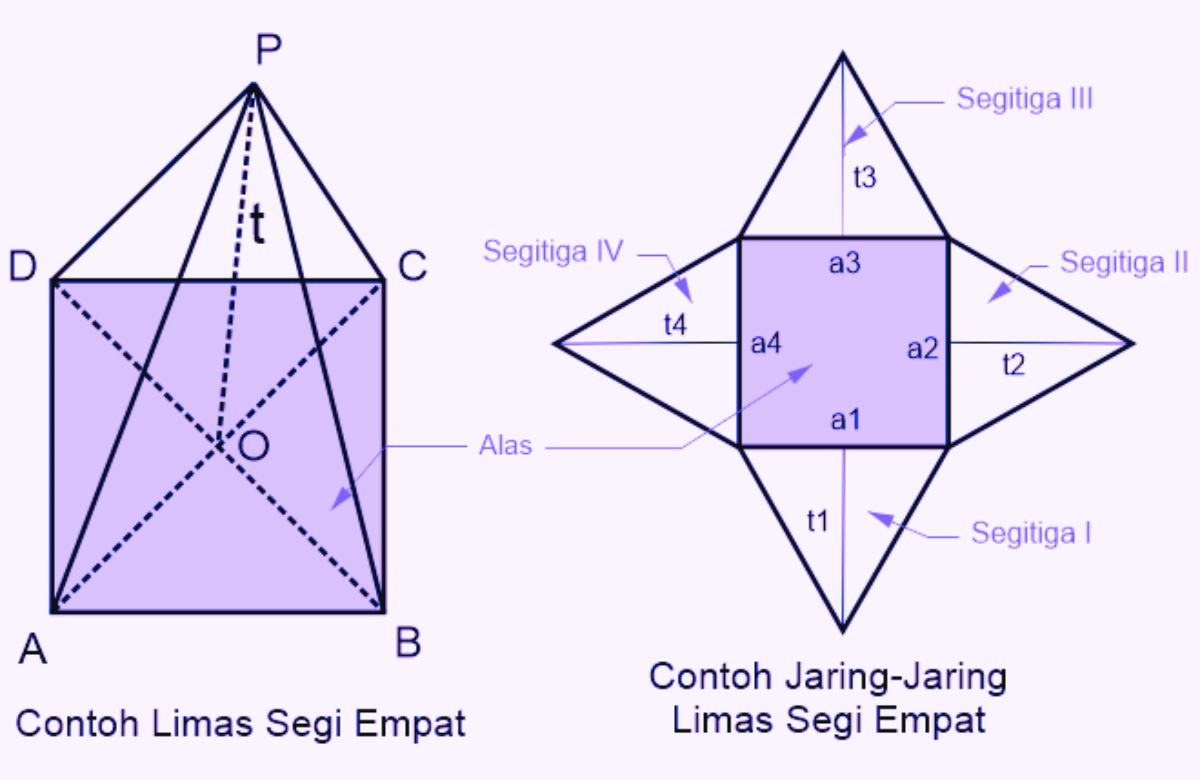
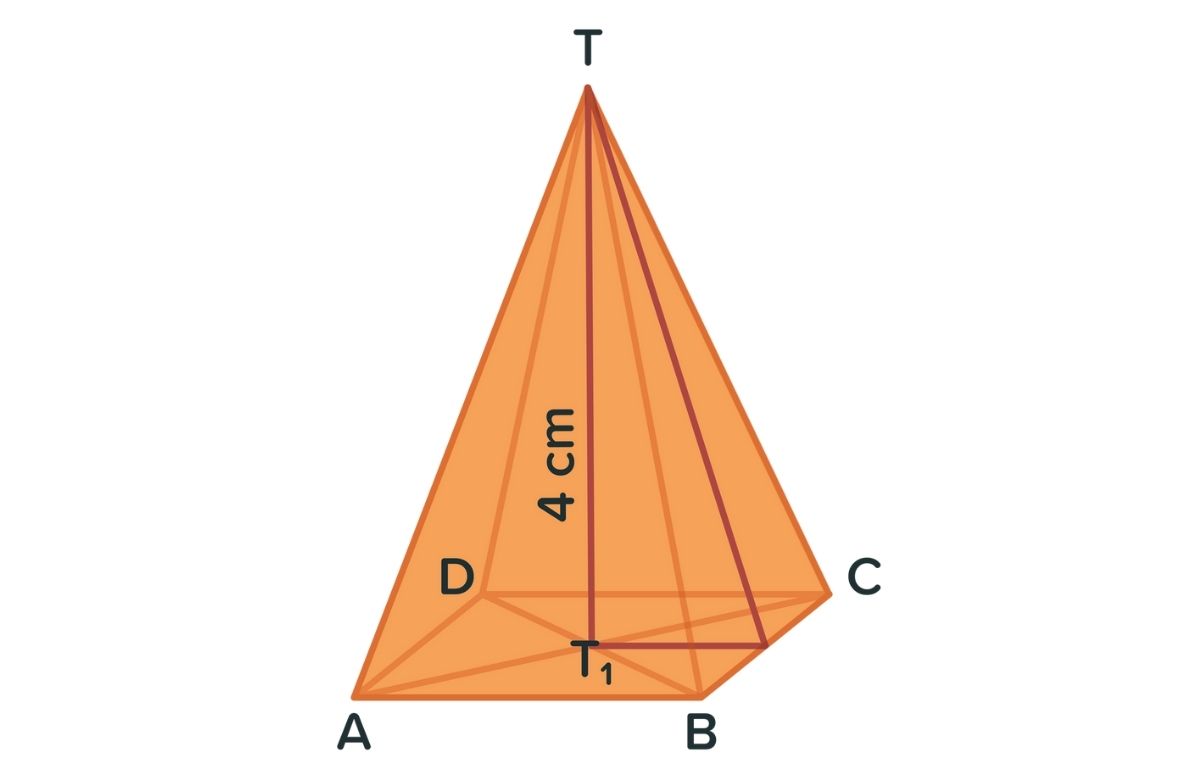
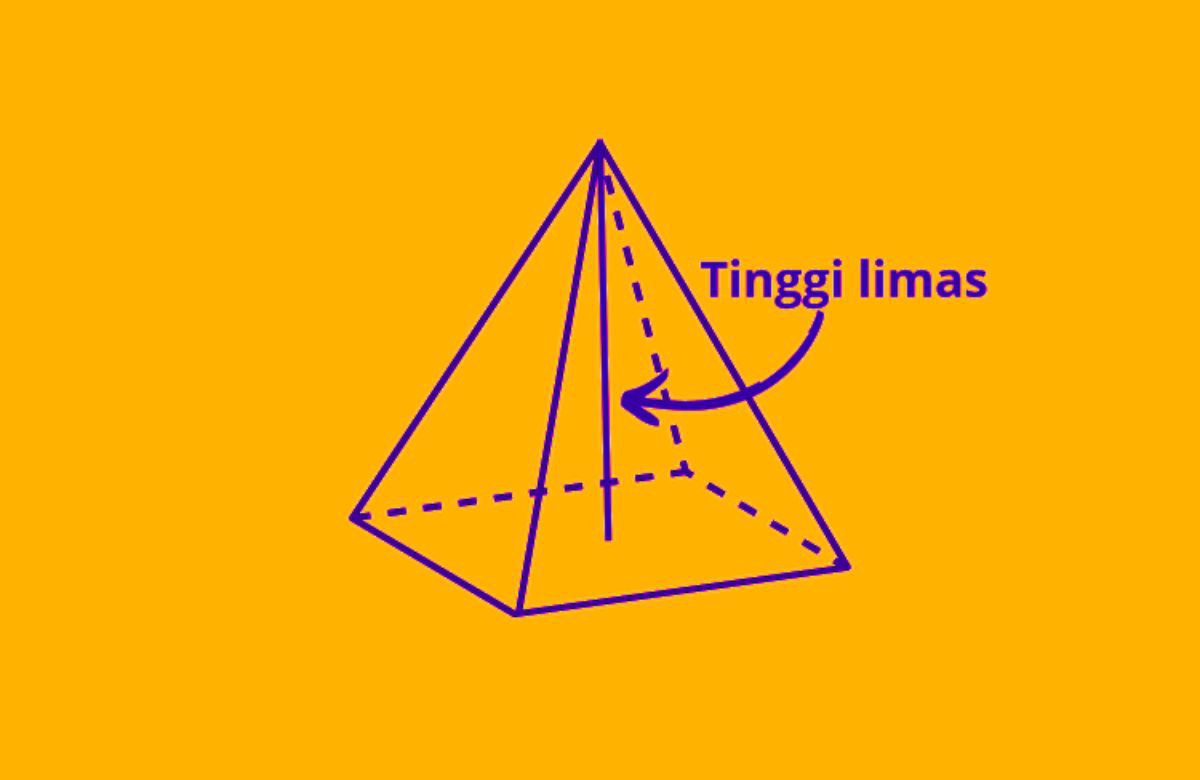
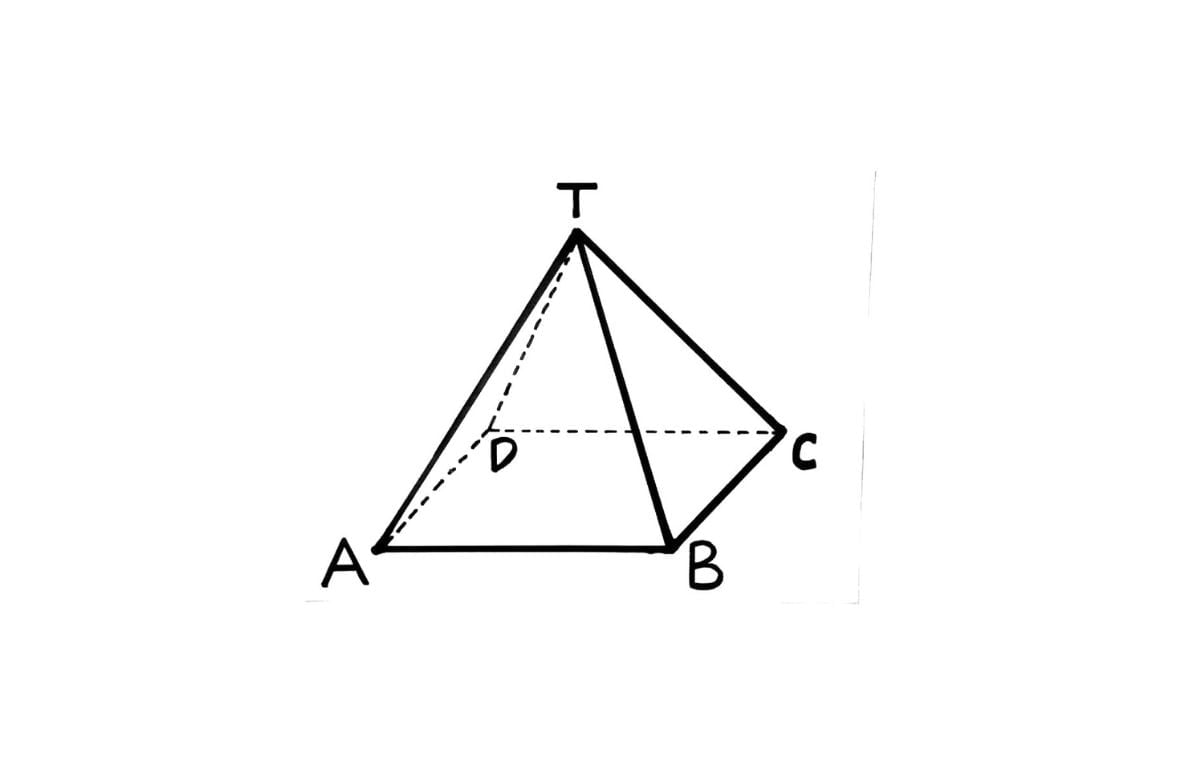
Limas segi empat adalah sebuah polihedron yang memiliki lima sisi, di mana satu sisi merupakan segi empat yang disebut dengan alas, dan empat sisi lainnya adalah segitiga yang disebut dengan sisi tegak.

Dalam bentuk Bangun Limas ini, alas berperan sebagai bidang datar yang terletak di bagian bawah dan berbentuk persegi atau persegi panjang.

Sementara itu, sisi tegak berupa empat segitiga dengan sisi-sisinya saling berhubungan di titik puncak atau apex. Limas persegi empat ini dapat memiliki bentuk yang bervariasi tergantung pada ukuran dan proporsi sisi-sisinya.

Salah satu sifat menarik dari Limas Segi Empat adalah memiliki satu sisi datar yang disebut bidang alas. Bidang ini memungkinkan limas untuk berdiri dengan stabil di permukaan datar.

Sementara itu, sisi tegak pada limas ini memiliki bentuk segitiga yang cenderung meruncing ke titik puncak. Titik puncak ini adalah salah satu ciri khas limas dengan alas segi empat yang membedakannya dari bentuk limas lainnya.

Keunikan lain dari limas beralas segi empat ini adalah jumlah sisi dan sudutnya. bentuk bangun ruang ini memiliki lima sisi atau lima sudut, yang terdiri dari satu sisi alas dan empat sisi tegak.

Setiap sisi tegak membentuk tiga sudut yang berjumlah 12 sudut pada keseluruhan limas. Sudut-sudut ini dapat bervariasi tergantung pada ukuran dan bentuk yang spesifik.

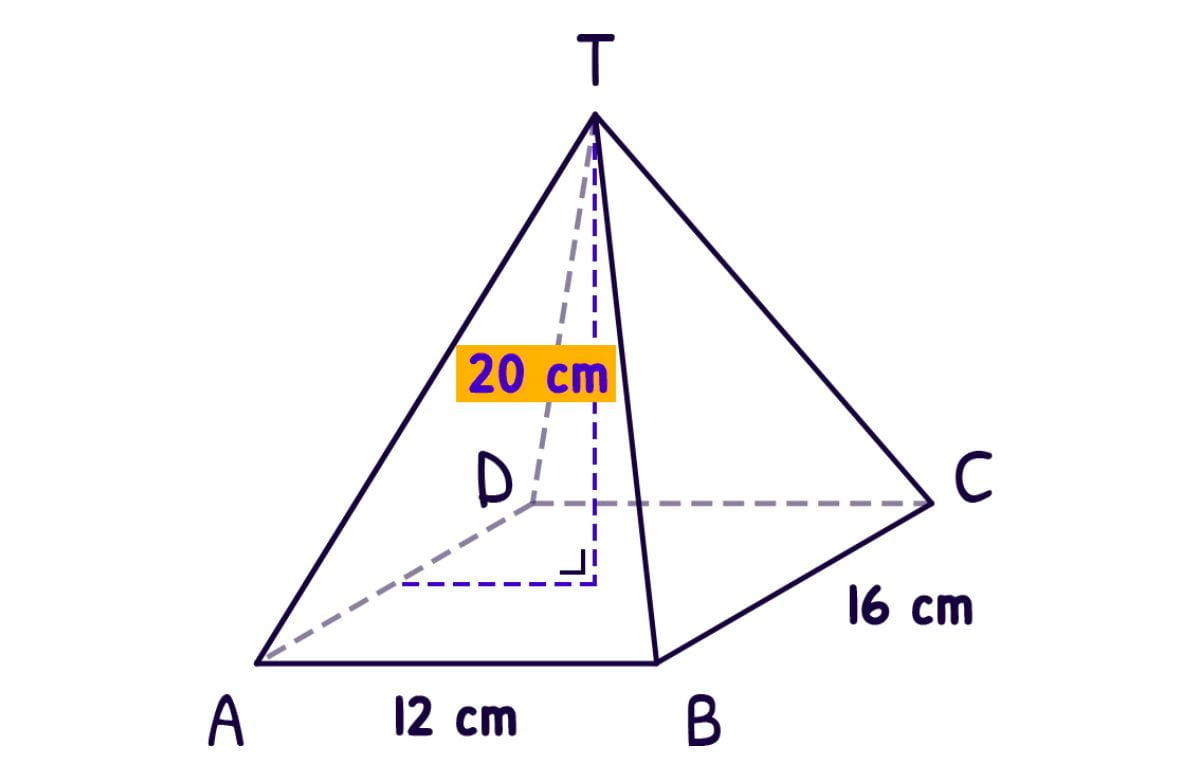
Limas segi empat juga dapat dihitung luas permukaan dan volume. Luas permukaan limas yang berbentuk segi empat dapat dihitung dengan menjumlahkan luas alas dan luas sisi-sisi tegaknya.

Sedangkan volume limas segi empat dapat dihitung dengan menggunakan rumus 1/3 x luas alas x tinggi. Dengan memahami rumus-rumus tersebut, kita dapat menghitung ukuran dan properti lainnya dari limas dengan bagian bawah berbentuk segi empat.

Contoh Gambar Limas Segi Empat (1)

Contoh Gambar Limas Segi Empat (2)

Contoh Gambar Limas Segi Empat: Mengenal Bentuk dan Sifatnya

Contoh Gambar Limas Segi Empat (5)

Contoh Gambar Limas Segi Empat (3)

Bentuk limas segi empat sering ditemui dalam berbagai konteks, termasuk arsitektur, geometri, dan bahkan dalam objek sehari-hari seperti piramida makanan.

Keindahan dan simetri yang dimiliki limas segi empat membuatnya menarik untuk dipelajari dan dipahami. Dalam matematika, limas segi empat menjadi salah satu objek yang sering digunakan dalam pembelajaran dan pengajaran konsep geometri.

Dengan mengenali limas segi empat dan memahami sifat-sifatnya, kita dapat lebih mengapresiasi keindahan geometri dan meningkatkan pemahaman kita tentang bentuk-bentuk yang ada di sekitar kita.

Limas segi empat merupakan salah satu bentuk yang menarik untuk dieksplorasi, dan pengetahuan tentangnya dapat membantu kita dalam memecahkan masalah dan menerapkan konsep-konsep matematika dalam kehidupan sehari-hari.

Selain itu, limas segi empat juga memiliki aplikasi praktis dalam berbagai bidang. Misalnya, dalam arsitektur, limas segi empat sering digunakan sebagai bentuk dasar dalam mendesain bangunan atau menara. Bentuk limas yang menonjol ke atas memberikan tampilan yang unik dan menarik pada bangunan tersebut.

Dalam bidang teknik dan konstruksi, limas segi empat digunakan sebagai model untuk memvisualisasikan berbagai struktur seperti kerucut lalu lintas atau tumpukan barang.

Dengan memahami sifat-sifat limas segi empat, para insinyur dan arsitek dapat merencanakan dan membangun struktur yang kokoh dan stabil.

Selain itu, limas segi empat juga dapat dijadikan bahan ajar yang menarik dalam pembelajaran matematika. Guru dapat menggunakan model limas segi empat fisik atau visualisasi komputer untuk membantu siswa memahami konsep luas permukaan, volume, dan sifat-sifat lainnya. Hal ini dapat meningkatkan minat dan keterlibatan siswa dalam pembelajaran matematika.

Baca juga: Sejarah Ilmu Matematika dan Pengertian Menurut para Ahli

Dalam dunia hiburan, limas segi empat juga menjadi inspirasi dalam karya seni, film, dan media lainnya. Contohnya, dalam film anime "Your Name" karya Makoto Shinkai, limas ini digunakan sebagai simbolisasi yang kuat dalam menceritakan kisah tentang takdir dan pertemuan dua karakter utama.

Secara keseluruhan, limas segi empat adalah bentuk geometri yang menarik dengan sifat-sifat uniknya. Mengenali dan memahami limas dengan bagian bawah berbentuk segi empat dapat membantu kita dalam memperluas pemahaman tentang geometri dan mengaplikasikannya dalam berbagai aspek kehidupan.

Dalam dunia matematika, limas segi empat merupakan salah satu objek yang menarik untuk dipelajari dan dieksplorasi, memberikan kita wawasan yang lebih dalam tentang bentuk dan sifat geometris.

Pewarta Nusantara - Dalam perkembangannya, matematika telah menjadi salah satu ilmu yang tak terpisahkan dari kehidupan manusia.

Para matematikawan berperan penting dalam menemukan pola, merumuskan dugaan baru, dan membangun kebenaran melalui metode deduktif yang ketat.

Sejarah Ilmu Matematika menjadi landasan yang mengungkap perjalanan panjang dan perkembangan disiplin ini.

Ilmu matematika mempelajari kuantitas, struktur, ruang, dan perubahan. Menurut Benjamin Peirce, seorang ahli matematika, matematika adalah "ilmu yang menjelaskan kesimpulan penting." Asal kata "matematika" berasal dari bahasa Yunani, dengan akar kata "mathema" yang berarti pengetahuan atau ilmu, serta kata "mathanein" yang berarti belajar atau berpikir.

Dalam esensinya, matematika adalah ilmu pengetahuan yang diperoleh melalui penalaran. Konsep matematika terbentuk melalui pemikiran manusia yang terkait dengan ide, proses, dan penalaran.

Disiplin ini memainkan peran krusial dalam memahami fenomena alam, menganalisis data, serta mengembangkan teknologi dan aplikasi di berbagai bidang kehidupan.

Sejarah ilmu matematika menjadi saksi perjalanan intelektual manusia dalam menggali pengetahuan dan mengembangkan sistem konseptual yang telah membentuk dunia modern yang kita kenal saat ini.
Jejak Agung Sejarah Ilmu Matematika: Dari Babilonia Hingga Al-Khawarizmi
 

Sampai saat ini, matematika masih menjadi momok yang ditakuti oleh banyak siswa di sekolah. Alasan utamanya adalah perhitungan yang banyak, rumus yang kompleks, dan materi yang padat.

Namun, tidak bisa dipungkiri bahwa matematika adalah mata pelajaran wajib yang memberikan dasar ilmu dan pola kognitif yang mempengaruhi mata pelajaran lainnya. Konsep matematika sebenarnya menjadi landasan bagi berbagai kegiatan sehari-hari kita.

Matematika membahas tentang ilmu kuantitas, struktur, ruang, dan ilmu hitung. Singkatnya, matematika adalah ilmu yang melibatkan berpikir dan penalaran.

Meskipun mungkin tidak disukai oleh sebagian orang, mengapa tidak mencoba mempelajari sejarah matematika untuk mengetahui asal usulnya? Pengetahuan tentang sejarah matematika dapat mengungkapkan bagaimana penemuan-penemuan dan perkembangan matematika yang terjadi sepanjang waktu, dan hal itu dapat memukau siapapun yang mempelajarinya.

Sebelum era modern dengan kemudahan penyebaran ilmu seperti sekarang, terdapat banyak contoh tertulis yang mencerminkan perkembangan matematika di berbagai wilayah.

Salah satu contohnya adalah Plimpton 332, Lembaran Matematika Rhind, dan Lembaran Matematika Moskwa. Ketiga naskah ini lebih fokus membahas teorema Pythagoras, yang menjadi salah satu pengembangan matematika tertua dan tersebar luas setelah aritmetika dasar dan geometri.

Melalui penelusuran sejarah matematika, kita dapat menyaksikan keajaiban di balik konsep-konsep ini dan memahami peranan pentingnya dalam pengembangan ilmu pengetahuan.

Ketika kita membahas sejarah matematika, kita tak dapat mengabaikan peran penting yang dimainkan oleh bangsa Mesopotamia, yang kini dikenal sebagai Irak, dalam pengembangan keseluruhan ilmu matematika.

Matematika Babilonia menjadi sangat terkenal pada masa itu, karena kawasan Babilonia menjadi tempat utama bagi perkembangan ilmu tersebut.

Salah satu pencapaian terkenal dari era ini adalah sistem bilangan seksagesimal (basis-60), yang menjadi dasar dalam perhitungan mereka.

Sistem bilangan seksagesimal ini memiliki implikasi yang luas dalam konsep matematika. Penggunaan angka 60 untuk menyatakan satu menit, 60 menit untuk satu jam, dan 360 (60 x 6) derajat untuk satu putaran penuh lingkaran, menjadi landasan bagi banyak perhitungan dan pengukuran hingga saat ini.

Selama masa-masa tersebut, konsep-konsep matematika baru terus berkembang, membawa manfaat yang besar bagi masyarakat.

Salah satu tokoh yang patut kita kenal adalah Muhammad bin Musa Al-Khawarizmi, yang dianggap sebagai Bapak Matematika Dunia. Penemuan luar biasanya menjadi tonggak penting dalam perkembangan matematika pada masanya, terutama penemuan aljabar dan konsep angka nol.

Al-Khawarizmi juga menciptakan penggunaan fungsi Trigonometri seperti Secans dan Tangen dalam penelitian trigonometri dan astronomi.

Pada masa muda, Al-Khawarizmi bekerja di Bayt al-Hikmah di Bagdad, di bawah pemerintahan Khalifah al-Ma'mun. Ia juga terlibat dalam Observatory, tempat di mana ilmu matematika dan astronomi dipelajari.

Selain itu, Al-Khawarizmi dipercaya sebagai pemimpin perpustakaan Khalifah, menunjukkan kontribusi dan keahliannya dalam bidang ilmu pengetahuan yang beragam.

Dalam dunia Islam, Al-Khawarizmi memperkenalkan angka-angka dan cara perhitungan yang berasal dari India. Ia juga dikenal sebagai penulis ensiklopedia yang mencakup berbagai disiplin ilmu.

Al-Khawarizmi menjadi tokoh yang pertama kali memperkenalkan konsep aljabar, perhitungan, serta berbagai konsep dan ilmu pengetahuan lainnya di bidang matematika yang masih kita pelajari hingga saat ini.

Selain bidang matematika, Al-Khawarizmi juga memiliki reputasi yang mengagumkan dalam ilmu Falak atau astronomi, yang mempelajari bintang-bintang dan melibatkan kajian tentang kedudukan, pergerakan, dan interpretasi yang berkaitan dengan benda langit tersebut.
Pengertian Ilmu Matematika Menurut Para Ahli

Berikut adalah rangkuman pandangan para ahli tentang matematika:

1. James dan James (1976): Matematika adalah pola pikir terorganisir, bukti logis, dan bahasa simbolik yang menggunakan istilah yang didefinisikan dengan cermat untuk representasi akurat.
2. Carl Friedrich Gauss: Gauss menyebut matematika sebagai "Ratu Ilmu" yang mencerminkan pengetahuan yang luas.
3. Johnson dalam Russefendi (1972): Matematika terdiri dari unsur-unsur yang tidak didefinisikan, definisi, aksioma, dan dalil-dalil yang berlaku secara umum. Oleh karena itu, matematika disebut sebagai ilmu deduktif.
4. Kline (1973): Matematika melibatkan penelitian tentang pola, hubungan, jalan berpikir, seni, bahasa, dan alat-alat matematika.
5. Russefendi: Matematika terorganisir melalui unsur-unsur yang tidak didefinisikan, definisi, aksioma, dan dalil-dalil yang berlaku secara umum, sehingga disebut ilmu deduktif.
6. Reys - dkk (1984): Matematika merupakan penelitian tentang pola, hubungan, jalan berpikir, seni, bahasa, dan alat-alat matematika.
7. Rising (1972): Matematika melibatkan pola pikir, pengaturan pola, logika, dan menggunakan istilah yang didefinisikan secara cermat dalam bahasa simbolik.
8. Yansen Marpaung: Matematika adalah ilmu yang mengikuti metode deduksi dalam perkembangan dan penggunaannya.
9. Kline (1973): Matematika bukan pengetahuan yang berdiri sendiri, tetapi digunakan untuk memahami dan mengatasi masalah dalam konteks sosial, ekonomi, dan alam. Logika menjadi dasar dalam pembentukan matematika.

Pandangan-pandangan tersebut mencerminkan bahwa matematika melibatkan pola pikir, logika, bahasa simbolik, dan penelitian tentang pola dan hubungan. Selain itu, matematika memiliki peran penting dalam memecahkan masalah dalam berbagai konteks kehidupan.

Menurut James dan James (1976), matematika dapat dianggap sebagai suatu pola pikir yang terorganisir, yang menggunakan bukti logis.

Matematika merupakan sebuah bahasa yang menggunakan istilah-istilah yang didefinisikan dengan cermat, memberikan representasi simbolik yang jelas dan akurat, dan lebih berfokus pada bahasa simbol daripada makna verbal.

Carl Friedrich Gauss menggambarkan matematika sebagai "Ratu Ilmu". Dalam bahasa Latin aslinya, Regina scientiarum, atau dalam bahasa Jerman Konigin der Wissenschaften, ungkapan tersebut menunjukkan bahwa matematika merupakan bidang pengetahuan yang tertinggi.

Menurut Johnson dalam Russefendi (1972), matematika terdiri dari unsur-unsur yang tidak didefinisikan, definisi, aksioma, dan dalil-dalil yang digunakan untuk membentuk argumen yang valid secara umum. Oleh karena itu, matematika sering disebut sebagai ilmu deduktif.

Kline (1973) melihat matematika sebagai sebuah kajian mengenai pola dan hubungan, yang melibatkan jalur pikir, seni, bahasa, dan alat-alat yang digunakan dalam penelitiannya.

Matematika mempelajari pola-pola yang ada dalam dunia ini dan menggali hubungan-hubungan yang tersembunyi di dalamnya.

Pandangan dari para ahli tersebut menggambarkan matematika sebagai suatu disiplin ilmu yang melibatkan pola pikir, bahasa simbolik, dan penggunaan bukti logis.

Matematika juga dianggap sebagai bidang pengetahuan yang tinggi, menghasilkan pemahaman tentang pola dan hubungan dalam dunia ini, serta memainkan peran penting dalam pemikiran deduktif.

Menurut Russefendi, matematika terdiri dari unsur-unsur yang tidak didefinisikan, definisi-definisi, aksioma-aksioma, dan dalil-dalil yang setelah dibuktikan kebenarannya berlaku secara umum. Oleh karena itu, matematika sering disebut sebagai ilmu deduktif.

Reys dan koleganya (1984) melihat matematika sebagai sebuah penelitian mengenai pola dan hubungan, sebuah jalan atau pola berpikir, serta sebuah seni, bahasa, dan alat-alat yang digunakan dalamnya.

Rising (1972) menggambarkan matematika sebagai pola pikir yang mengatur pola, membuktikan logika. Matematika menggunakan istilah-istilah yang didefinisikan dengan cermat, memberikan representasi akurat melalui simbol-simbol yang padat, dan lebih berfokus pada bahasa simbol daripada ide verbal.

Menurut Yansen Marpaung, matematika merupakan sebuah ilmu yang dalam perkembangannya menggunakan metode deduksi.

Baca juga: Lucius Annaeus Seneca (4-65M) Sang Penulis Produktif dan Penasehat Imperial

Kline (1973) berpendapat bahwa matematika bukanlah pengetahuan yang dapat menjadi sempurna untuk dirinya sendiri, melainkan matematika terutama digunakan untuk membantu orang memahami dan mengatasi masalah dalam bidang sosial, ekonomi, dan alam. Matematika tumbuh dan berkembang melalui proses berpikir, dan logika menjadi dasar pembentukannya.

Pandangan dari para ahli tersebut menggambarkan matematika sebagai disiplin ilmu yang mengandung unsur-unsur deduktif, penelitian pola dan hubungan, logika, dan penggunaan bahasa simbolik.

Matematika juga memiliki peran penting dalam memahami dan memecahkan masalah dalam berbagai bidang kehidupan.